【蜗牛棋牌】小白教程 | “凯利公式”与德州扑克比赛（上）

凯利公式与德州扑克比赛（上）

上个世纪前叶，美国出现了很多数学天才，包括香农，索普，纳什等。他们的很多成就，其实都来自于博彩。他们的研究领域包括二十一点，轮盘赌等。甚至计算机的发明，都与博彩业有关。而这些人中，本来是物理学家的凯利，41岁就英年早逝，却是对博彩业影响最大的科学家。

凯利公式的发明，是二十世纪对博彩业和投资金融业影响最大的数学事件之一。而凯利公式的灵感来自于上世纪初遍布美国的外桩赌马。

凯利公式的策略，是针对当时赌马的内部消息。如何在不确定的内部消息中下注获得最大收益而不破产，是凯利公式解决的问题。

除可将长期增长率最大化外，此方程式不允许在任何赌局中，有失去全部现有资金的可能，因此有不存在破产疑虑的优点。方程式假设货币与赌局可无穷分割，而只要资金足够多，在实际应用上不成问题。

而写了一本旷世奇书《决胜二十一点》的数学家索普，就是凯利公式的一个实践者，他利用凯利公式策略，出入美国各大赌场，让赌场输得莫名其妙。最后被赌场宣布为不受欢迎的人。

记得以前我说过，凯利公式可以用于德州扑克比赛。一些不懂装懂的人说我是胡说八道。其实他们根本没听懂我的意思。如果说我跟那些不懂装懂的人有什么本质区别，就一点，我的数学水平可以甩开他们的可怜数学水平好几条街！

凯利公式后来被应用最多的，是股票投资领域。用来资金管理。所以，有人误以为凯利公式是专门用来资金管理的。包括德州扑克比赛的资金管理。其实，凯利公式最初的发明，是用于赌马。正如前面提到的，凯利公式是说，如果我们有获胜的可能（内幕消息是其中最直接的），我们应该如何下注，才能保证不破产而获得最理想的收益？

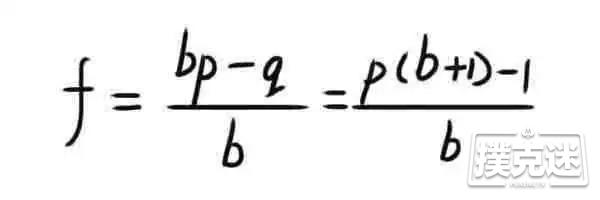
凯利的结论是，最佳投注比例为：

期望值/赔率。

公式很简单，F=(bp-q)/b

F=下注资金比例

p=胜率

q=输率即（1-p）

b=赔率

所以，凯利公式是一个无风险投注指数。

举个例子说吧，如果你持有AKo，你看到对手持有JQo，底池赔率为1.5。也就是说，在你有60%胜率的情况下，赔率为1赔1.5的情况下，你投入有效筹码的多少比例，收益是没有风险的（前提已经有了，就是你有60%的胜率，你的投入是正EV行为）？

根据凯利公式，你的投入比例为：

F=(1.5*60%-40%)/1.5=33.3%。也就是说，你投入筹码量的33.3%是无风险的。

其原理是，如果你的EV值为投入量的50%。你的赔率为150%（赔率1.5）的话，你如果分三次投入你的筹码，你就可以实现你的赔率了。这样，你避免了一次投入被40%输率输掉的风险。你通过三次投入，实现你的50%的EV值，跟你一次投入全部筹码相比，风险更小。而收益一样。

当然，凯利公式不是你获利最大的投注方式。因为如果你一次投入所有筹码，一但你获胜，你得到到不是50%的EV值，而是150%的回报。然而，你一单输了，就血本无归破产。

从以上例子我们看到，凯利公式是一个EV/赔率的公式。它说明了投入量的最佳比例。德州扑克比赛中，我们经常会遇到这样的难题，就是我们如何在风险和收益之间找到平衡。凯利公式可以帮助解决这个问题。

就上面的例子来说，如果我们有三倍于对手的筹码，我们的投入是没有风险的。因为我们可以用三次这样的投入，获得最大的EV回报。问题是，我们经常没有这样的筹码量，那么，凯利公式就没有用了么？

有用的！凯利公式其实给了我们一个无风险投注的比例指数。我们完全可以用凯利公式来判断我们的风险有多大。比如，在底池只有1.5bb的情况下，我们持有AKo，我们知道对手是JJ。我们持有30bb，对手全下，我们是否应该跟住？

凯利公式告诉我们，我们的无风险投入指数为：

赔率b=31.5/30=1.05

胜率p=50%(大致如此)

我们的无风险投入指数：

(1.05*50%-50%)/1.05=2.38%

也就是说，我们投入筹码的2.38%是无风险的。而我们现在要投入30bb，即100%筹码，去赢2.5%的EV值。这是巨大的风险。我们没有必要这样做。凯利公式可以作为德州扑克比赛筹码投入量的风险指数。这个毋庸置疑。

然而，认真的读者马上会提出一个问题。比赛哪里有无风险投注的机会？这样的机会这么少，凯利公式还有用么？当然有用。凯利公式其实可以作为一个风险指数，我们可以利用他来判断比赛中具有破坏性牌局的风险（比如全下弃牌阶段风险），同时，我们可以根据比赛的重要性，比赛的重要阶段，来制定一个我们能承受的风险指数，与凯利公式进行对照。就可以指导我们投注。

举例子说，红龙比赛进入第三天，我们持有40bb筹码，场上还有50人。平均筹码30bb。我们认为自己的水平在比赛中属于上游。没有必要跟对手拼命。但是，在什么样的情况下，我们要接一个30bb对手的全下呢？

另外举个例子对照。比如，同样是这个比赛。这时候我们在庄位偷一个盲注，基本上对手大小盲50%不防守的话，我们用任意牌下注2.5bb偷盲注，我们偷一次盲注地收益是0.75bb（假设有前注，底池2.5bb。粗略计算）。那么我们是冒着2.5bb风险偷取0.75bb收益。按比例，这相当于我们用30bb赢取9bb。偷盲的这个风险相比我们冒险用30bb赢取9bb的风险要小得多！这可能是锦标赛偷盲收益最典型的例子。当然，我们仅仅靠偷盲，可能无法满足我们筹码增长的需要。我们关键时刻需要冒险跟对手跑马，以获得筹码迅速增长。但是根据场上的形势，偷盲有如此收益，我们是否应该接一个30bb筹码的Allin的结论就有据可寻了。

假设，我们有40bb筹码，对手有30bb，我们持有AKo，我们在前位open2.5bb对手在庄位全下30bb，我们是否应该跟住？假设底池盲注加前注2.5bb，我们的赔率是：

(30bb+2.5bb+2.5bb)/27.5bb=1.27

假设我们估计对手范围为99+ AJs+ AQo+，我们AK胜率49.8%，

请问，我们是否应该跟住？

根据凯利公式，我们的无风险投入比例为：

(1.27*49.8%-50.2%)/1.27=0.13/1.27

=10.3%

凯利公式告诉我们，我们用AK跟住一个5%的范围，底池赔率为1.27，我们的无风险投入量为10%左右。我们用27.5bb接对手allin，冒27.5bb风险，获得13%EV值，即3.59bb左右，是具有巨大风险的波动。那么，我们在什么情况下是可以冒这个险的呢。

如先前所说，我们用偷盲的方式，相当于用30bb可以偷取9bb，我们可以用凯利公式计算一下，这个风险是多大。

我们偷盲的赔率是EV值9bb/30bb

(每偷取0.75bb，冒2.5bb风险，冒30bb风险，偷取9bb)=30%

赔率大致为39/30=1.3

凯利指数F=0.3/1.3=23%

假定我们把凯利风险指数最小确定为23%，那么10%的风险指数就不能接对手的全下。

上面的例子中，如果我们接对手全下27.5bb的无风险指数达到23%，我们的底池赔率需要达到1.87左右。

(b*49.8%-50.2%)/b=23%

b=1.87

以上我们只是提供了一种思考方法。我们在比赛中如何应用凯利公式？因为比赛是获取筹码增长与避免死亡波动的平衡。所以我们掌握凯利公式，对我们控制筹码波动是有用的。

具体来说，什么样的比赛我们用什么样的无风险指数作为我们在具有潜在破坏性的牌局中的行动指引，我们还需要进一步探讨，在以后的文章中我会给出更准确的答案。